伪随机数推算

前言

以往遇到的考察伪随机数的题目都相对比较简单 无非就是通过seed来推算出后续的随机数 但是这次的核心在于 seed不可控且不可知的情况下 如何通过seed生成的伪随机数 来推算出后续的随机数

rand函数源码分析

先来弄懂 rand函数究竟是如何通过seed来生成随机数的
以下代码均从 https://codebrowser.dev/glibc/ 摘录

/* Return a random integer between 0 and RAND_MAX.  */
int
rand (void)
{
  return (int) __random ();
}

内部进而调用了__random函数 跟进一下看看

__random (void)
{
  int32_t retval;

  __libc_lock_lock (lock);

  (void) __random_r (buf: &unsafe_state, result: &retval);

  __libc_lock_unlock (lock);

  return retval;
}

重点关注一下__random_r函数 unsafe_state结构体作为参数传输 返回值存储于retval

static struct random_data unsafe_state =
{
    /* FPTR和RPTR是指向状态信息的两个指针，一个前指针和一个后指针。
       这两个指针始终相隔rand_sep个位置，因为它们在状态信息中循环。
       （是的，这意味着我们可以只用一个指针，但是这种方式的random代码更高效）。
       这两个指针的位置是从调用initstate(1, randtbl, 128)的位置开始：
       （后指针rptr的位置实际上是0（如上面在初始化randtbl时解释的那样），
       因为状态表指针被设置为指向randtbl[1]（如下面解释的那样）。）*/

    .fptr = &randtbl[SEP_3 + 1],    // SEP_3 = 3
    .rptr = &randtbl[1],

    /* 以下内容是指向状态信息表的指针、当前生成器的类型、当前多项式的度数和两个指针之间的间隔。
       注意，为了random的效率，我们记住状态信息的第一个位置，而不是第零个位置。
       因此，访问state[-1]是有效的，它用于存储R.N.G.的类型。
       另外，我们记住最后一个位置，因为这比每次索引以查找最后一个元素的地址来判断前后指针是否已经回绕更高效。 */

    .state = &randtbl[1],

    .rand_type = TYPE_3,    // 3
    .rand_deg = DEG_3,      // 3
    .rand_sep = SEP_3,      // 3

    .end_ptr = &randtbl[sizeof(randtbl) / sizeof(randtbl[0])]
};

根据注释可以得到 fptr和rptr是指向状态信息的前后指针 并且虽然rptr的起始是randtbl[1]但是实际上是0
为了理解这一描述 我们先来看一下randtbl数组的内容

static int32_t randtbl[DEG_3 + 1] =
{
    TYPE_3,

    -1726662223, 379960547, 1735697613, 1040273694, 1313901226,
    1627687941, -179304937, -2073333483, 1780058412, -1989503057,
    -615974602, 344556628, 939512070, -1249116260, 1507946756,
    -812545463, 154635395, 1388815473, -1926676823, 525320961,
    -1009028674, 968117788, -123449607, 1284210865, 435012392,
    -2017506339, -911064859, -370259173, 1132637927, 1398500161,
    -205601318
};

该数组存储着内部状态信息 用于随机数的生成
通过randtbl数组的注释 我们可以得知上文中 后指针的位置为0的原因

Initially, everything is set up as if from: ↪
    initstate(1, randtbl, 128); ↪
   Note that this initialization takes advantage of the fact that srandom ↪
   advances the front and rear pointers 10*rand_deg times, and hence the ↪
   rear pointer which starts at 0 will also end up at zero; thus the zeroth ↪
   element of the state information, which contains info about the current ↪
   position of the rear pointer is just ↪
    (MAX_TYPES * (rptr - state)) + TYPE_3 == TYPE_3.

后指针在初始化的时候指向第一个元素 所以第一个元素存储的是后指针当前位置的信息
接着我们回到unsafe_state结构体
其还定义了其他成员 用来记录生成器类型 随机次数 随机间隔
此外还记录了最后一个元素的位置
接下来分析一下__random_r函数

int __random_r(struct random_data *buf, int32_t *result)
{
    int32_t *state;

    if (buf == NULL || result == NULL)
        goto fail;

    state = buf->state;

    if (buf->rand_type == TYPE_0)
    {
        int32_t val = ((state[0] * 1103515245U) + 12345U) & 0x7fffffff;
        state[0] = val;
        *result = val;
    }
    else
    {
        int32_t *fptr = buf->fptr;
        int32_t *rptr = buf->rptr;
        int32_t *end_ptr = buf->end_ptr;
        uint32_t val;

        val = *fptr += (uint32_t)*rptr;
        /* Chucking least random bit. */
        *result = val >> 1;
        ++fptr;
        if (fptr >= end_ptr)
        {
            fptr = state;
            ++rptr;
        }
        else
        {
            ++rptr;
            if (rptr >= end_ptr)
                rptr = state;
        }
        buf->fptr = fptr;
        buf->rptr = rptr;
    }
    return 0;

fail:
    __set_errno(EINVAL);
    return -1;
}

参考注释可以得知 生成器有两种类型 TYPE_0是使用旧的线性同余法 另外一个则是使用精巧三项式算法
先来看较为简单的前者 state[0]指向randtbl数组的第二个元素 将其乘以1103515245 U代表无符号整数 随后加上12345 最后进行与运算
这里清空了符号位 并且只保留低31位
随后更新state[0]以及result

接下来看后者
开始先将结构体的成员赋值给对应的局部变量(下面 前指针和后指针所指向的数值 为了方便描述 均采用缩写为前后指针
接着将后指针加上前指针 其和重新赋值给了前指针以及val变量
随后的注释比较耐人寻味 其说舍弃最不随机的位
下一条指令对val右移了一位 相当于val除2 结果取整
这里说的最不随机的位指的是最低1位
就拿线性同余运算举例
其运算式为

val = ((state[0] * 1103515245U) + 12345U) & 0x7fffffff

这里使用state[0]默认的值379960547代入
可以编写这样一个测试程序

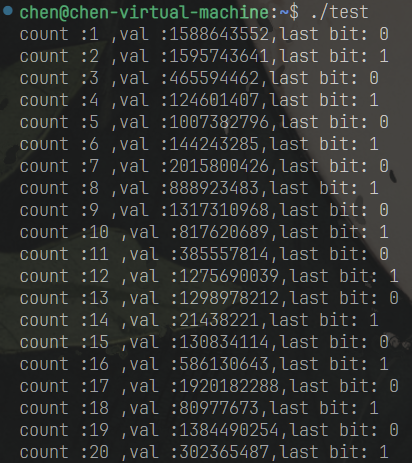
#include <stdio.h>
#include <stdlib.h>
#include <signal.h>
#include <string.h>
int main(){
    int32_t state = 379960547;
    int32_t val =0;
    int time=1;
    int bit =0;
    for(int i=0;i<20;i++){
        val = ((state * 1103515245U) + 12345U) & 0x7fffffff;
        bit = val&1;
        state = val;
        printf("count :%d ,val :%d,last bit: %d\n",time,val,bit);
        time ++;
    }
}

最后得到的结果为

可以看到最后一个bit为0和1交替 呈现出一定规律 所以称之为最不随机的位
说回正文 在进行了右移运算后 自增了前指针
如果前指针超过了数组的最后一个元素 那么就重置前指针 使其重新指向randtbl数组的第二个元素
如果没有超过 再自增后指针 如果后指针超过 那么就重置后指针 同上

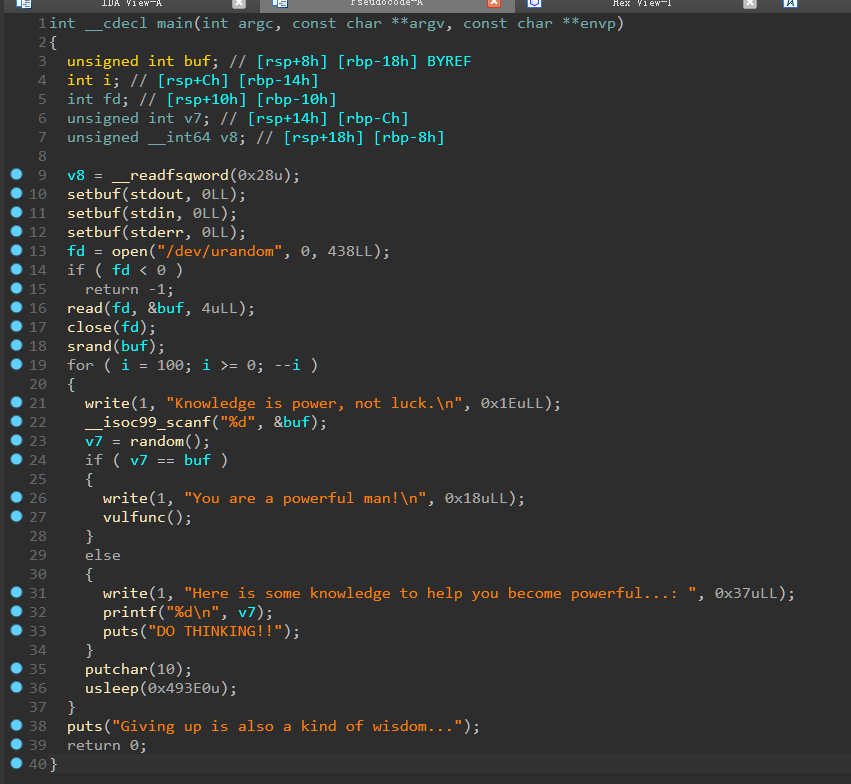
如何预测随机数

经过上面的源码分析
可以大概清楚随机数的生成逻辑
state数组从randtbl数组的第二个元素开始 也就是说state一共有31个元素
前指针初始指向s[3] (这里将state数组缩写成s)
后指针初始指向s[0]
那么我们这里就可以得到随机数数组o的第一个元素为
o[0] = (s[3]+s[0])>>1
随后前指针和后指针均自增
随着推移 前指针会率先来到s数组的最后一个元素s[30]
根据源码推断 超过了s[30]后 就会重新赋值成s[0]
但是这里要注意 在随机数生成后 后指针与前指针之和会赋值给前指针
所以我们这里的s[?]只是一个代号 而非具体的值
也就是o[28] = (s[0]+s[28])>>1
同理 o[31] = (s[3]+s[0])>>1
如果拆分开成 s[3]=s[3]+s[0],s[0] = s[0]+s[28]
o[31]的值就有两种可能性
第一种为o[31] = o[0]+o[28]
第二种为o[31] = o[0]+o[28]+1
见下面表格

s[0]	s[3]	s[28]	o[31]
奇	奇	奇	1
奇	奇	偶	1
奇	偶	奇	1
偶	奇	奇	2
奇	偶	偶	2
偶	偶	奇	1
偶	偶	偶	1

可以看出是第一种可能性的概率为七分之五
也就是说 如果我们得到了o[0]和o[28] 我们就有比较大的概率预测出o[31]
同理 可以继续往下推 o[1]和o[29] 可得出o[32]等等
o[n] = o[n-31]+o[n-3]或o[n] = o[n-31]+o[n-3]+1
由于本人数学水平不高 所以无法想出怎么百分百预测 感兴趣的可以自己尝试(顺顺教教我

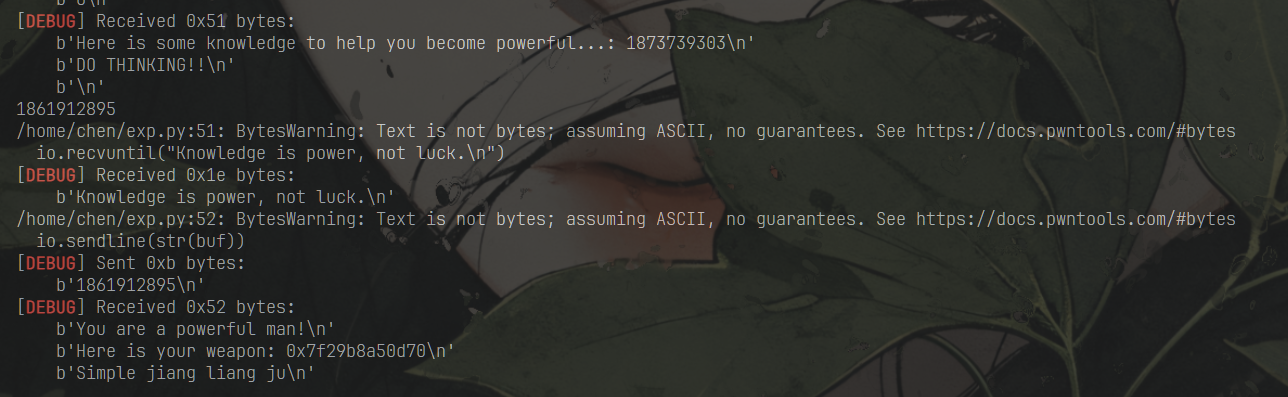
实际演示

以上面这题来举例 seed无法得知也无法覆盖
一共有101次机会
在猜数错误后 会提供正确的随机数
所以我们只需要保留o[0]和o[28]
就可以得出第32个随机数o[31]

o = []
buf = 0
for i in range(31):
    io.recvuntil("Knowledge is power, not luck.\n")
    io.sendline(b'0')
    io.recvuntil('Here is some knowledge to help you become powerful...: ')
    c = int(io.recvuntil("\n",drop = True))
    o.append(c)
buf = o[0]+o[28]
print(buf)
io.recvuntil("Knowledge is power, not luck.\n")
io.sendline(str(buf))
io.recv()
io.recv()

成功得到正确的数值